
The divisor, 3.92, in the formula above would be replaced by 2 × 2.0639 = 4.128.įor moderate sample sizes (say between 60 and 100 in each group), either a t distribution or a standard normal distribution may have been used. For example the t value for a 95% confidence interval from a sample size of 25 can be obtained by typing = tinv(1-0.95,25-1) in a cell in a Microsoft Excel spreadsheet (the result is 2.0639). Relevant details of the t distribution are available as appendices of many statistical textbooks, or using standard computer spreadsheet packages.

The numbers 3.92, 3.29 and 5.15 need to be replaced with slightly larger numbers specific to the t distribution, which can be obtained from tables of the t distribution with degrees of freedom equal to the group sample size minus 1. If the sample size is small (say less than 60 in each group) then confidence intervals should have been calculated using a value from a t distribution.
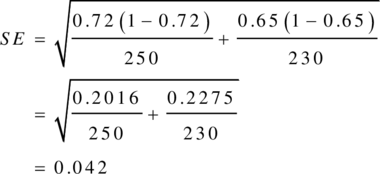
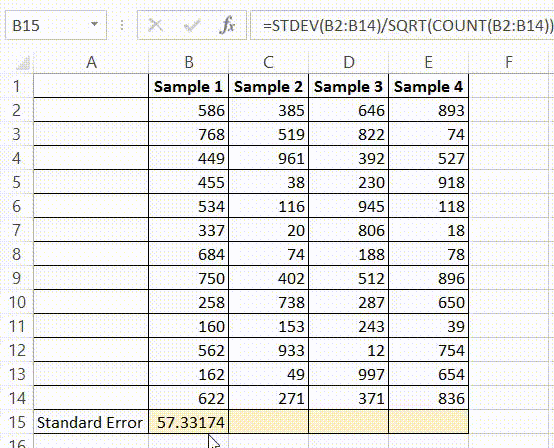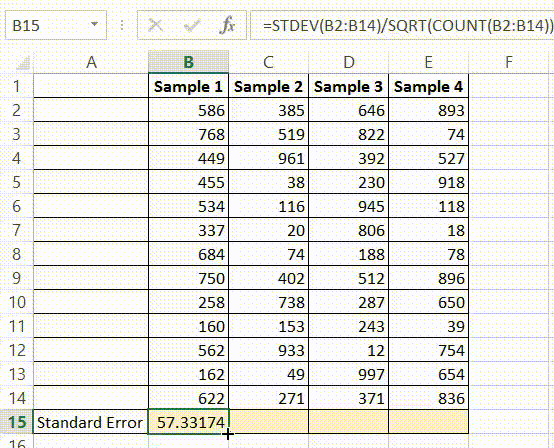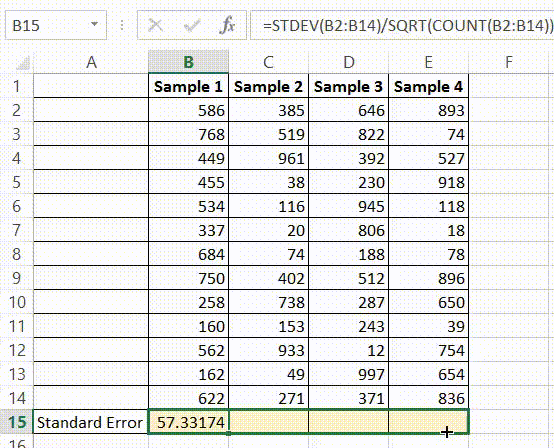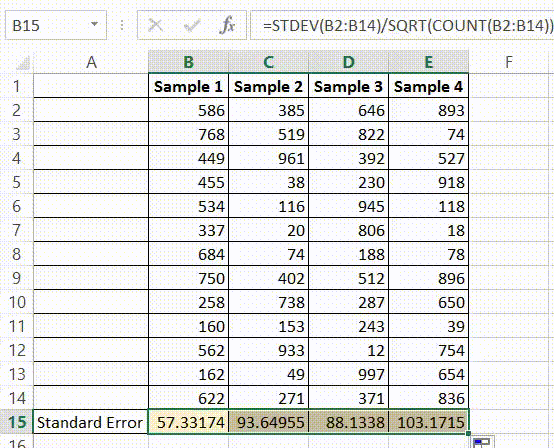
The standard deviation for each group is obtained by dividing the length of the confidence interval by 3.92, and then multiplying by the square root of the sample size:įor 90% confidence intervals 3.92 should be replaced by 3.29, and for 99% confidence intervals it should be replaced by 5.15. If the sample size is large (say bigger than 100 in each group), the 95% confidence interval is 3.92 standard errors wide (3.92 = 2 × 1.96). Most confidence intervals are 95% confidence intervals. Again, the following applies to confidence intervals for mean values calculated within an intervention group and not for estimates of differences between interventions (for these, see Section 7.7.3.3). When making this transformation, standard errors must be of means calculated from within an intervention group and not standard errors of the difference in means computed between intervention groups.Ĭonfidence intervals for means can also be used to calculate standard deviations. 7.7.3.2 Obtaining standard deviations from standard errors and confidence intervals for group meansĪ standard deviation can be obtained from the standard error of a mean by multiplying by the square root of the sample size: For the current version, please go to /handbook/current. Which is the same value computed previously.This is an archived version. Formulas comparable to the ones for the population are shown below.

square. The only difference is that the denominator is N-2 rather than N, since two parameters (the slope and the intercept) were estimated in order to estimate the sum of squares The difference between the means of two samples, A and B, both randomly drawn from the same normally distributed source population, belongs to a normally distributed sampling distribution whose overall mean is equal to zero and whose standard deviation ('standard error') is equal to.Similar formulas are used when the standard error of the estimate is computed from a sample rather than a population. Since many standard error calculations involve Standard Deviation (SD), the following two formulas are the calculations of. Where ρ is the population value of Pearson's correlation There is a version of the formula for the standard error in terms of Pearson's correlation: We will be using the numpy available in python, it provides std() function to calculate the standard error of the mean. Therefore, the standard error of the estimate is: The Standard error of the mean for a sample is calculated using below formula: Standard error of the mean (SEM) s / n.The last column shows that the sum of the squared errors of prediction is 2.791.Therefore, the predictions in Graph A are more accurate than in Graph B.Īssume the data below are the data from a population of five X-Y pairs.You can see that in graph A, the points are closer to the line then they are in graph B.The graphs below shows two regression examples.Y-Y' - differences between the actual scores and the predicted scores. S est is the standard error of the estimate, is a measure of the accuracy of predictions.is closely related to this quantity and is defined below:.


 0 kommentar(er)
0 kommentar(er)
